Перевод чисел из одной системы счисления в другую

Что такое система счисления

Система нумерации — это символьный метод записи чисел, представление чисел с помощью символов.

Символы, используемые для записи числа, называются цифрами.

• даёт представления множества чисел (целых или вещественных)
• даёт каждому числу уникальное представление (или, по крайней мере, стандартное представление)
• отражает алгебраическую и арифметическую структуру чисел.

Разные народы в разное время использовали разные системы нумерации. Следы древних систем счисления можно найти и сегодня в культурах многих народов. Вавилоняне восходят к делению часа на 60 минут и угла на 360 градусов. В Древнем Риме существовала традиция записывать числа I, II, III и т.д. в латинской нотации. Для англосаксов — измерение десятками: в году 12 месяцев, в футе 12 дюймов, день делится на 2 периода по 12 часов.

По современным данным, развитые системы нумерации впервые появились в Древнем Египте. Для записи чисел египтяне использовали иероглифы один, десять, сто, тысяча и т.д. Все остальные числа записывались с помощью этих иероглифов и акта сложения. Недостатками этой системы были невозможность записи больших чисел и ее неудобство.

В итоге десятичная система оказалась самой популярной системой счисления. Он состоит всего из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и позиция, в которой она находится. В числе 444 три одинаковые цифры обозначают количество единиц, десятков и сотен. В числе 400, с другой стороны, первая цифра обозначает количество сотен. Два 0 сами по себе не вносят никакого вклада в число, а нужны только для того, чтобы указать положение цифры 4.

2.10. Как производятся арифметические операции в позиционных системах счисления

Рассмотрим основные арифметические операции: сложение, вычитание,
умножение и деление. Правила выполнения этих операций в десятичной системе
хорошо известны — это сложение, вычитание, умножение столбиком  
и  деление углом. Эти правила применимы и ко всем другим позиционным
системам счисления. Только таблицами сложения и умножения надо пользоваться
особыми для каждой системы.

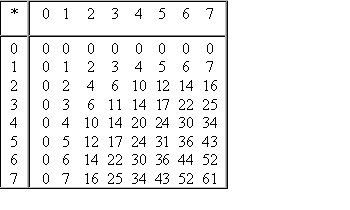
Таблицы сложения легко составить, используя Правило Счета.  

Сложение в двоичной системе

Сложение в восьмеричной системе

Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает
избыток, то он переносится влево.     Пример 1. Сложим числа 15 и 6 в различных системах
счисления.

     

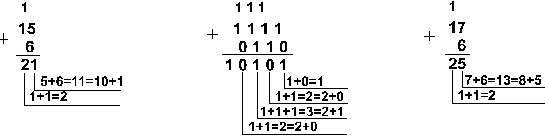
Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516.  Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 2 = 16+4+1=21,  258 = 2. 81 + 5. 8 = 16 + 5 = 21,  1516 = 1. 161 + 5. 16 = 16+5 = 21.

Пример
2.

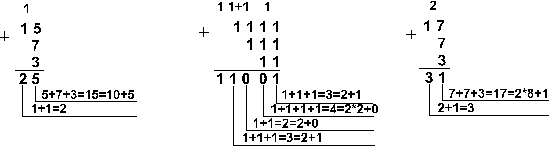
Шестнадцатеричная: F16+716+316

Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916.  Проверка: 110012 = 24 + 23 + 2 = 16+8+1=25, 318 = 3. 81 + 1. 8 = 24 + 1 = 25,  1916 = 1. 161 + 9. 16 = 16+9 = 25.

Пример 3.

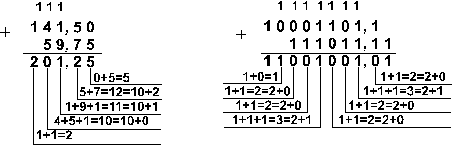
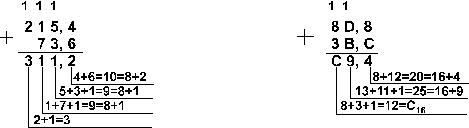  Ответ: 141,5 + 59,75 = 201,25₁₀ =
11001001,01₂ = 311,2₈ = C9,4₁₆Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 27 + 26 + 23 +
2 + 2-2 = 201,25 311,2₈ = 3.
82 + 1. 81 + 1. 8 +
2. 8-1 = 201,25 C9,4₁₆ = 12. 161 + 9. 16 + 4. 16-1 = 201,25

Пример 4. ₂₈₁₆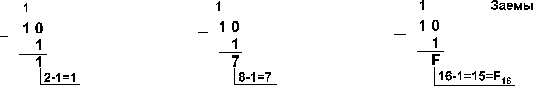Пример 5.₂₈₁₆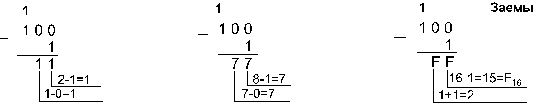Пример 6.

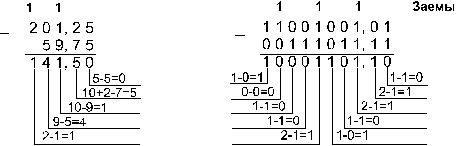
  Ответ: 201,25₁₀ — 59,75₁₀ =
141,5₁₀ = 10001101,1₂ = 215,4₈ =
8D,8₁₆. Проверка. Преобразуем полученные разности к
десятичному виду: 10001101,1₂ = 27 + 23 +
22 + 2 + 2-1 = 141,5; 215,4₈ =
2. 82 + 1. 81 +
5. 8 + 4. 8-1 =
141,5; 8D,8₁₆ = 8. 161 + D. 16 + 8. 16-1 = 141,5.

Выполняя умножение многозначных чисел в различных позиционных системах
счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но
при этом результаты перемножения и сложения однозначных чисел необходимо
заимствовать из соответствующих рассматриваемой системе таблиц умножения и
сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Пример 7.

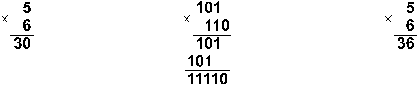Ответ: 5. 6 = 30₁₀ = 11110₂
= 36₈. Проверка. Преобразуем полученные произведения к
десятичному виду: 11110₂ = 24 + 23 +
22 + 21 = 30; 36₈ = 3. 8
1 + 6. 8 = 30.    
Пример 8. Перемножим числа 115 и 51.

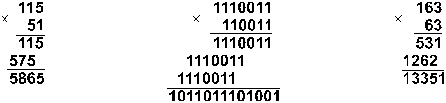Ответ: 115. 51 = 5865₁₀ =
1011011101001₂ = 13351₈. Проверка. Преобразуем
полученные произведения к десятичному виду: 1011011101001₂ =
212 + 210 + 29 + 27 + 26
+ 25 + 23 + 2 = 5865; 13351₈ =
1. 84 + 3. 83 +
3. 82 + 5. 81 +
1. 8 = 5865.

Пример 9.

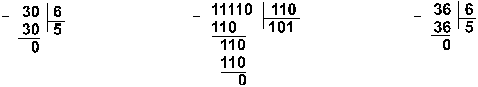Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.
    Пример 10. Разделим
число 5865 на число 115.

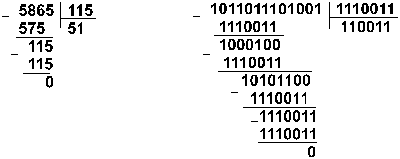
Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ =
63₈. Проверка. Преобразуем полученные частные к
десятичному виду: 110011₂ = 25 + 24 +
21 + 2 = 51; 63₈ = 6.
81 + 3. 8 = 51.  
  Пример 11. Разделим число 35 на
число 14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ =
2,4₈. Проверка. Преобразуем полученные частные к
десятичному виду: 10,1₂ = 21 + 2 -1 = 2,5;
2,4₈ = 2. 8 + 4.
8-1 = 2,5.

Правила перевода из одной системы счисления в другую.

Далее последовательно разбирается перевод систем счисления.

1. Перевод целых десятичных чисел в любую другую систему счисления.

Число нужно разделить на новое основание системы счисления. Первый остаток от деления — это и есть первая младшая цифра нового числа. Если частное от деления меньше или равно новому основанию, то его (частное) нужно снова разделить на новое основание. Деление нужно продолжать, пока не получим частное меньше нового основания. Это есть старшая цифра нового числа (нужно помнить, что, например, в шестнадцатиричной системе после 9 идут буквы, т.е. если в остатке получили 11, нужно записать его как B).

Пример («деление уголком»): Переведем число 173₁₀ в восьмеричную систему счисления.

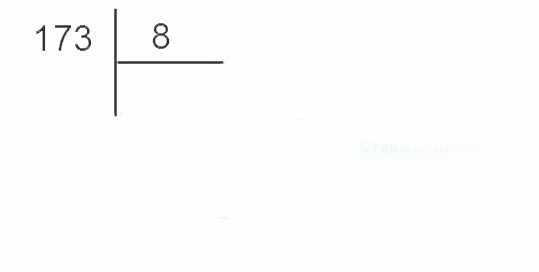
Таким образом, 173₁₀=255₈

2. Перевод правильных десятичных дробей в любую другую систему счисления.

Число нужно умножить на новое основание системы счисления. Цифра, перешедшая в целую часть — старшая цифра
дробной части нового числа. для получения следующей цифры дробную часть получившегося произведения опять нужно
умножать на новое основание системы счисления, пока не произойдет переход в целую часть. Умножение продолжаем,
пока дробная часть не станет равна нулю, либо пока не дойдем до указанной в задаче точности («… вычислить
с точностью, например, двух знаков после запятой»).

Пример: Переведем число 0,65625₁₀ в восьмеричную систему счисления.

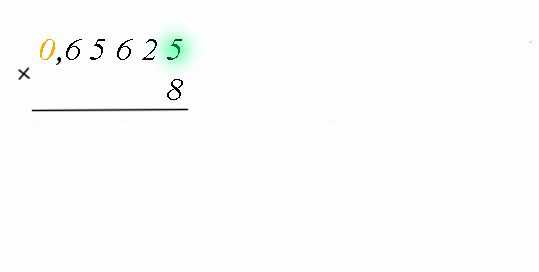
Таким образом, 0,65625₁₀=0,52₈

3. Перевод смешаных десятичных чисел в любую другую систему счисления.

Переводим отдельно целую часть, отдельно дробную — записываем в одно число.

Пример: Переведем число 17,25₁₀ в восьмеричную систему счисления.

По аналогии с пунктом 1: 17₁₀ = 21₈

По аналогии с пунктом 2: 0,25₁₀ = 0,2₈

«Склеиваем» два числа и получаем ответ: 17,25₁₀ = 21,2₈.

4. Перевод чисел из любой системы счисления в десятичную.

Числа необходимо представить в разложении по степеням той системы счисления, в которой находится число, при чем
цифры числа необходимо записать в десятичном эквиваленте. Найти арифметическую сумму.

Пример: Переведем число 1011,01₂ в десятичную систему счисления.

1) Чтобы представить число в разложении по степеням, нужно найти запятую и проставить «карандашиком»
влево и вправо от запятой степени над цифрами числа (слева — неотрицательные степени, т.е. начинаем с нуля;
справа — отрицательные, начиная с -1):

13 02 11 1,
0-1 1-2₂

2) Далее умножаем каждую цифру на основание системы счисления, в которой находится число, возведенное
в соответствующую «подписанную» степень (помним, что любое число в нулевой степени — это единица):

1011,01₂ = 1*23 + 0*22 + 1*21 +
1*2 + 0*2-1 + 1*2-2 = =
8 + 0 + 2 + 1 + 0 + 1/22 = 11 + 1/4 = 11 + 0,25 = 11,25₁₀

Ответ: 11,25₁₀.

5. Перевод чисел из восьмеричной системы счисления в двоичную.

Каждую цифру восьмеричного числа нужно заменить соответствующей двоичной триадой ( * * * ) —
например, для цифры 7 — 111, для 3 — 011. Незначащие нули можно отбросить.

Пример: Переведем число 274,06₈ в двоичную систему счисления.

Просто заменяем все числа триадами:

2 7 4, 0 6 -> 010 111 100, 000 110

274,06₈ = 10111100,00011₂

Ответ: 10111100,00011₂.

6. Перевод чисел из двоичной системы счисления в восьмеричную.

Несложно догадаться, что на этот раз мы просто разбиваем число на триады и заменяем
восьмеричными цифрами (помним, что разбивать начинаем «от запятой» влево и вправо; там, где не хватает дополняем незначащими нулями).

Пример: Переведем число 1111,0110011₂ в восьмеричную систему счисления.

Разбиваем на триады и заменяем:

001’111,011’001’100 -> 1’7,3’1’4

1111,0110011₂ = 17,314₈

Ответ: 17,314₈.

Откуда же появились эти «триады»?

Да это же степень, в которую нужно возвсти двойку, чтобы получить основание 8!

Очевидно, что для шестнадцатиричной системы счисления появятся тетрады («тетра» — четыре) и т.д.

4 = 22
8 = 23	Триады
16 = 24	Тетрады
32 = 25

7. Перевод чисел из двоичной системы счисления в шестнадцатиричную и обратно.

Перевод чисел из двоичной системы счисления в шестнадцатиричную и обратно выглядит так же,
как и для пути «восьмеричная двоичная». Отличие состоит лишь в использовании тетрад ( * * * * ).

Пример: Переведем число CD2,04₁₆ в двоичную систему счисления.

Разбиваем и заменяем:

C’D’2, 0’4 -> 1100’1101’0010, 0000’0100

CD2,04₁₆ = 110011010010,000001₂

Ответ: 110011010010,000001₂.

Двоичная система счисления

Эта система счисления свое название получила в результате того, что содержит в своем основании всего две цифры – $0$ и $1$. Таким образом, число $2$ и его степени $2, 4, 8$ и т.д. играют особую роль. Самая правая цифра числа показывает число единиц, следующая – число двоек, следующая — число четверок и т.д.

В двоичной системе счисления для формирования числа используются всего две цифры: $0$ и $1$. Пределом разряда является $1$, и как только при счете разряд достигает своего максимального значения, он обнуляется, а при этом образуется новый разряд. Ниже в таблице приведены соответствия двоичных и десятичных чисел.

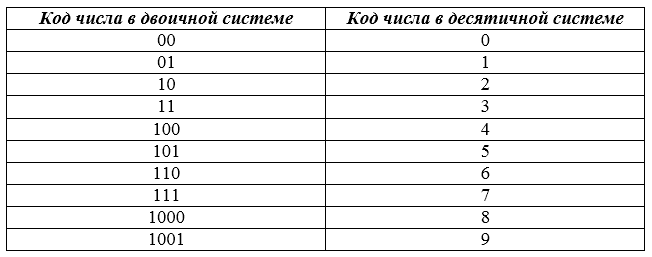Рисунок 1.

Замечание 2

Используя двоичную систему счисления, можно закодировать любое натуральное число, представляя его как последовательность нулей и единиц.
В двоичном виде можно представить не только числа, но и любую другую информацию: тексты, изображения, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что оно легко реализуется технически.

Именно на принципе двоичного кодирования работает вся вычислительная техника: $1$ означает, что электрический сигнал прошел, а $0$ – сигнал отсутствует. Наглядно это можно рассмотреть на примере перфокарт, которые использовались в вычислительных машинах первых поколений. Как уже упоминалось выше: в перфокартах пробивались отверстия в соответствующих рядах и столбцах цифр, таким образом, кодировались и сохранялись программы, поскольку жестких дисков, и тем более оптических, в те времена не было. Затем программы считывались при помощи электрического сигнала, который, если проходил в отверстие, значит, это был код $1$ и, наоборот, если не проходил сигнал – это был код $0$. Аналогичным способом в настоящее время записываются оптические диски при помощи лазерного луча, прожигающего невидимые микроотверстия на поверхности специальных дисков. Принцип считывания закодированной информации с диска аналогичен предыдущему.

Из всего вышесказанного можно сделать вывод, что компьютер «понимает» всего два числа: $0$ и $1$. И именно один двоичный разряд и является минимальной единицей измерения памяти компьютера, которая называется «бит», т.е. бит – это ячейка памяти компьютера, в которую можно записать $1$ или $0$.

Другой единицей измерения информации является байт.

Байт – это восемь подряд расположенных битов. Общее количество комбинаций двоичных значений в байте равно $28 = 256$.

$1 \ байт = 8 \ битам$;
$1 \ Кб = 210 \ байта = 1024 \ байта$;
$1 \ Мб = 210 \ Кбайт = 1024 \ Кбайта$;
$1 \ Гб = 210 \ байта = 1024 \ килобайта$;
$1 \ Тб = 210 \ гигабайта = 1024 \ гигабайта$.

Замечание 3

Достоинства двоичной системы счисления заключаются в ее простоте, благодаря которой она широко используется в технике. Устройства, работающие в двух состояниях (включено, выключено), наиболее помехоустойчивы, и, как следствие, более надежны.

Шестнадцатиричная система счисления

Давайте посмотрим определение шестнадцатеричной системы счисления, а потом расшифруем его:

Что это значит. Если в десятичной системе для записи любого числа используется десять символов (основание 10) — цифры от нуля до девяти, то в шестнадцатиричной системе используется шестнадцать символов (основание 16), в качестве которых обычно используются десятичные цифры от нуля до девяти (всего десять) и латинские буквы от A до F (всего шесть — A, B, C, D, E и F).

К примеру, число девять и в десятичной и шестнадцатиричной системах, будет записываться одинаково — 9. А вот число десять (в десятичной — 10), в шестнадцатиричной системе будет выглядеть так — «А».

Шестнадцатиричная система счисления используется потому, что в микроконтроллерах (как и всей компьютерной технике) минимальной единицей памяти является 8-битный байт, значения которого очень удобно записывать именно в шестнадцатиричной системе. Такое использование началось на заре развития компьютерной техники с систем фирмы IBM, где вся документация использовала шестнадцатеричную систему.

Для того, чтобы случайно не спутать числа в десятичной системе с числами в шестандцатиричной, для последней используется определенный синтаксис:
— используется префикс (запись перед числом):   «0х» или знак «зеленного» — «$», или такой знак — «#», или
— в конце числа ставят букву «h»

К примеру, десятичное число 10 в шестнадцатиричной системе может выглядеть так:- A- OxA- $A- Ah- #A

Встречается и другой синтаксис.

Давайте посмотрим соответствие шестандцатеричных чисел десятичным:
1 – 1
5 – 5
10 – А
200 – С8

Ну а выражение «позиционная система счисления», или «позиционная нумерация», означает, что значение цифры в записи числа зависит от его позиции (единица в самом конце числа — просто единица, а если она вторая справа, то уже — десяток).

Перевод числа в разные системы счисления

Как отмечалось выше, системой счисления является метод представления чисел. Одно и то же число можно представить в разных видах. К примеру, число 200 в привычной всем десятичной системе имеет несколько другое отображение в других системах счисления, а именно:

1. 11001000 в двоичной системе счисления.
2. 310 в восьмеричной системе счисления.
3. C8 в шестнадцатеричной системе счисления.

Чтобы указать тип системы счисления при записи числа применяется так называемый используется нижний индекс, который следует поставить после числа:

$200_{10} = 11001000_2 = 310_8 = C8_{16}$

Десятичная система счисления применяется в повседневной жизни человека и считается самой распространенной. Все числа, которые необходимы для вычислений, представлены в этой системе. В любом разряде таких чисел может располагаться лишь одна цифра от нуля до девяти.

Двоичная система счисления в основном применяется в вычислительной технике. Для записи чисел в этой системе применяются всего две цифры, а именно, нуль и единица.

Восьмеричная система счисления тоже иногда используется в вычислительной технике. Для записи чисел в этой системе применяются цифры от нуля до семи.

Шестнадцатеричная система счисления, пожалуй, является самой распространённой современном компьютерном оборудовании. С её помощью может быть указан цвет, например:

FF0000 обозначает красный цвет.

Для записи чисел в этой системе применяются цифры от нуля до девяти, а также буквы A, B,C,D,E,F, обозначающие соответственно числа 10,11,12,13,14,15.

Выполнить преобразование числа из какой-либо системы счисления в десятичную систему возможно путём осуществления следующих действий:

1. Все разряды числа следует умножить на $X_n$, где X является основанием исходного числа, а n определяет номер разряда.
2. Выполнить суммирование полученных значений.

Формула этих действий имеет следующий вид:

$abc_x = (a*x^2 + b*x^1 + c*x^0)_{10}$

Ниже приведены примеры подобных преобразований:

$567_8 = (5*8^2 + 6*8^1 + 7*8^0)_{10} = 375_{10}$

$110_2 = (1*2^2 + 1*2^1 + 0*2^0)_{10} = 6_{10}$

$A5_{16} = (10*16^1 + 5*16^0)_{10} = 165_{10}$

Для перевода числа из десятичной системы счисления в другие системы, необходимо выполнить следующие действия:

1. Выполнить деление десятичного число на основание системы счисления, в которую необходимо осуществить перевод, и записать остатки от деления.
2. Записать полученные остатки в обратном порядке, что и даст в итоге искомое число.

Рассмотрим пример перевода числа $375_{10}$ в восьмеричную систему:

1. 375 / 8 = 46 (остаток семь)
2. 46 / 8 = 5 (остаток шесть)
3. 5 / 8 = 0 (остаток пять)
4. Выполняем запись остатков, что в итоге даёт число 5678

Рассмотрим способы преобразования числа из двоичной системы счисления в восьмеричную систему. Первый способ:

1. Чтобы выполнить перевод из двоичной системы счисления в восьмеричную, следует разбить двоичное число на группы по три цифры справа налево.
2. В последней группе, которая слева, вместо недостающих цифр следует ставить слева нули.
3. Для каждой сформированной группы нужно выполнить умножение всех разрядов на $2^n$, где n является номером разряда.

Ниже приведён пример такого преобразования:

$1101_2 = (001) (101) = (0*2^2 + 0*2^1 + 1*2^0) (1*2^2 + 0*2^1 + 1*2^0) = (0+0+1) (4+0+1) = (1) (5) = 15_8$

Второй способ предполагает следующие действия:

1. Аналогично первому способу необходимо разбить число на группы.
2. Вместо преобразований в скобках следует просто заменить сформированные триадные группы на необходимые цифры восьмеричной системы счисления, с помощью следующей таблицы триад:

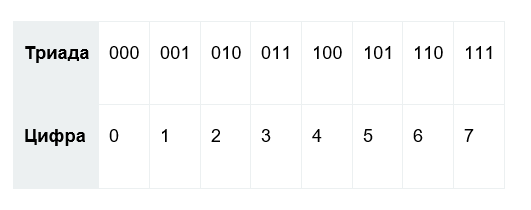Рисунок 1. Таблица. Автор24 — интернет-биржа студенческих работ

Ниже приведён пример преобразования по этому способу:

$10111010_2 = (010) (111) (010) = 272_8$

Рассмотрим способы преобразования числа из двоичной системы счисления в шестнадцатеричную систему. Первый способ заключается в выполнении следующих операций:

1. Выполнить разбиение числа на группы по четыре цифры справа налево.
2. Последнюю (левую) группу следует при необходимости дополнить ведущими нулями.
3. Внутри каждой сформированной группы следует осуществить умножение каждой цифры на $2^n$, где n является номером разряда.
4. Выполнить сложение результатов.

Ниже приведён пример такого преобразования:

$11010_2 = (0001) (1010) = (0*2^3 + 0*2^2 + 0*21 + 1*2^0) (1*2^3 + 0*2^2 + 1*2^1 + 0*2^0) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A_{16}$

Второй способ предполагает выполнение следующих операций:

1. Выполнить разбиение числа на группы по четыре цифры.
2. Заменить сформированные тетрадные группы на необходимые цифры из шестнадцатеричной системы, применяя тетрадную таблицу.

Ниже приведён пример такого преобразования:

$101111100_2 = (0001) (0111) (1100) = 17C_{16}$

Зачем нужна двоичная система

Двоичная система выглядит очень непривычно и числа, записанные в ней, получаются огромными. Зачем она вообще нужна? Разве компьютеры не могут работать с привычной нам десятичной системой?

Оказывается, когда-то они именно так и работали. Самый первый компьютер ENIAC, разработанный в 1945 году, хранил числа в десятичной системе счисления. Для хранения одной цифры применялась схема, которая называется кольцевым регистром, она состояла из десяти радиоламп.

Чтобы записать все числа до миллиона — от 0 до 999 999 — надо шесть цифр, значит, для хранения таких чисел нужно целых 60 ламп.

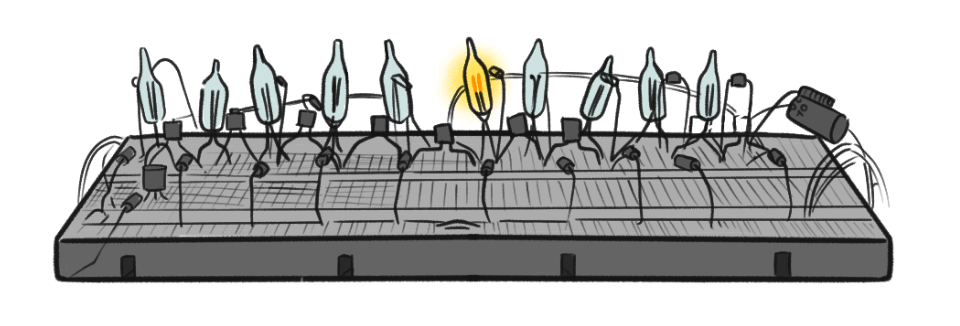
Инженеры заметили, что если бы они кодировали числа в двоичной системе, то для хранения таких же больших чисел им бы потребовалось всего двадцать радиоламп — в три раза меньше!

Первое преимущество двоичных чисел — простота схем

Второе, и не менее важное — быстродействие. Сложение чисел, хранящихся в кольцевом регистре, требует до десяти тактов процессора на каждую операцию

Сложение двоичных чисел можно выполнить за один такт — то есть в десять раз быстрее.

Группа инженеров, создавших первый компьютер, в 1946 году опубликовала статью, где обосновала преимущество двоичной системы для представления чисел в компьютерах. Первой среди авторов была указана фамилия американского математика Джона фон Неймана. Поэтому сейчас принципы проектирования компьютеров называются архитектурой фон Неймана, хотя это не совсем справедливо по отношению к другим изобретателям компьютера.

При разработке программы с двоичной записью столкнуться довольно сложно: компьютер в подавляющем большинстве случаев сам переводит двоичные числа в десятичные и обратно. Можно долго писать код, даже не подозревая, что внутри компьютера данные хранятся каким-то особым образом.

Зачем изучать двоичную систему, если компьютер делает всю работу за нас? Иногда программистам приходится писать программы, которые работают напрямую с оборудованием. Например, разработчики игр должны знать, как работают видеокарты, чтобы сделать компьютерную графику быстрее. А разработчики операционных систем понимают, как устроены диски, чтобы надежно хранить данные.

Программы, которые работают с железом напрямую, называются системными или низкоуровневыми. Для их создания разработчик должен понимать, как устроен компьютер. Поэтому изучение систем счисления позволяет программисту расширить свой профессиональный диапазон и стать специалистом широкого профиля.

Поэтому для того, чтобы писать сложные системные программы, нужно понимать, как устроена двоичная система счисления.

Применение восьмеричной системы счисления

В прошлом веке выпускались компьютеры, в которых использовались 12-ти, 24-х и 36-битные слова. Это, например, модель ICT 1900 (1964 год), а также PDP-8, выпущенная в 1965 году — это коммерчески довольно успешная модель миникомпьютера в своё время. Кроме того, некоторые мейнфреймы от компании IBM использовали восьмеричную систему. В компьютерах, размер машинного которых кратен тройке, очень удобно использовать систему с основанием восемь, поскольку всегда все биты из слова можно представить в виде целого количества цифр в восьмеричной системе. Например, слово из 24-х бит, можно записать в виде 8-ми восьмеричных чисел.

Если говорить про использование восьмеричной системы в жизни людей, то известно, что в индейских языках Юки (Калифорния) и Паме (Мексика) использовалась данная система. Индейцы считали предметы не по количеству пальцев на руках, а по количеству промежутков между ними.

Поделиться в соц. сетях:

Перевод чисел из одной системы счисления в другую

Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h. Удобно различать два случая.

В первом случае
и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования
состоит в представлении числа в виде
многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления
с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный
приём иллюстрируют следующие примеры:

.

.

В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.

Во втором случае ()
удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел
и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части
переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.

Перевод целых чисел

Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе. Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:

.

Для нахождения значений разделим
этот многочлен на h:

.

Как видно, младший разряд
, то есть , равен первому остатку.
Следующий значащий разряд определяется
делением частного на h:

.

Остальные также
вычисляются путём деления частных до тех пор, пока
не станет равным нулю.

Для перевода целого числа из s-ичной системы счисления в h-ичную
необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h)
до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит
последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в
последовательности, обратной их получению.

Пример 1. Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.

Решение:

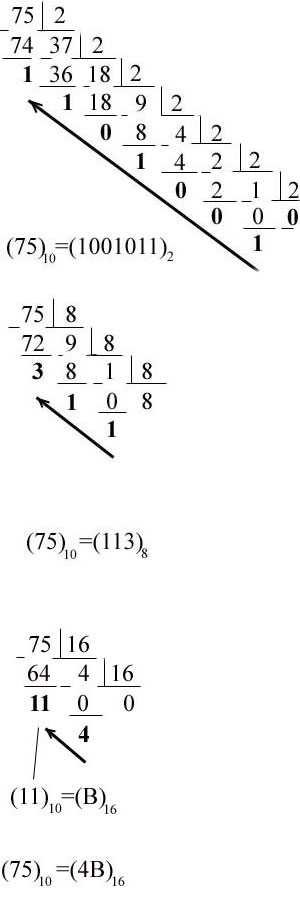
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат,
то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления
в другие системы.

Перевод правильных дробей

Правильную дробь ,
имеющую в системе с основанием s вид ,
можно выразить в системе счисления с основанием h как многочлен вида

Старшая цифра может быть
найдена умножением этого многочлена на h, т.е.

Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения. Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь
по основанию h конечным набором цифр.

Для перевода правильной дроби из системы счисления
с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части
получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных
произведений дают последовательность цифр дроби в h-системе счисления.

Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения
не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в
h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления
будет последовательности целых частей полученных произведений, записанных в порядке их получения и
изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p
знаков после запятой равняется .

Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.

* В двоичную систему:

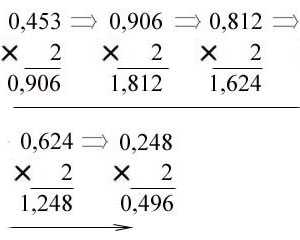
Ответ:

** В восьмеричную систему:

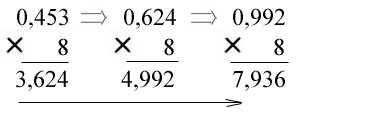
Ответ:

*** В шестнадцатеричную систему:

Ответ: так как , то

Поделиться с друзьями

Заключение

Люди изобрели разные способы записывать числа. Мы называем их системами счисления. Привычный для нас способ записи называется десятичной системой счисления.

Компьютеры, которые работали в десятичной системе, оказались сложными и медленными. Хранение чисел в двоичной системе позволило упростить схемы и ускорить работу компьютеров.

Обычно нам не нужно знать, как именно компьютер хранит числа, потому что он умеет переводить их в привычную нам форму. Но если мы хотим разрабатывать программы, которые работают с оборудованием напрямую — системные утилиты или компьютерные игры, — нужно разобраться, как устроены двоичная и шестнадцатеричная системы.

Существует ряд алгоритмов, которые помогают перевести число из одной системы в другую, но они достаточно запутанные. Проще использовать Google.

Двоичная запись чисел очень громоздкая, поэтому программисты предпочитают записывать числа в шестнадцатеричной системе счисления. Восьмеричная запись чисел сейчас используется очень редко.

Вы можете конвертировать числа из системы в систему на своём любимом языке программирования.